

For proving that for every NFA, there is an equivalent DFA in 1959, the Turing Award was given to Rabin and Scott. Initial state be the first row state.Create the transitions from the table.ĭeterministic Finite Automata (DFA) vs Non-deterministic Finite Automata (NFA)ĭeterministic Finite Automata (DFA) is equivalent to Nondeterministic Finite Automata (NFA). Construct a new DFA with minimal states by declaring each cell in the above list to be a state.For every state i, define a list of cells which are not marked.Mark a cell (a, b) with X if (a, b) does not have a mark and there exists a transition from cell (a, c) and (b, c) and one of them has the mark.Initialize table with X for the cells (i, j) which involve one of the states i or j as accept state.Make a 2D table where rows and columns are denoted by different states of DFA A.Remove all states that cannot be reached from the stating state of DFA A.The steps of Minimization algorithm for DFA are as follows: There exists an algorithm to minimize the number of states in a given DFA. DFA A is minimal if there is no DFA B equivalent to A which has less number of states than A.DFA A is equivalent to DFA B if L(A) = L(B).Therefore, in these lines, you can prove that the given Language L is not Regular Language using DFA. This results in a contradiction as M should accept either both or none.Show that there exists a string z such that xz belongs to L but yz does not belong to L.Use Pigeonhole principle to show that there exists two distinct strings x and y which will reach the same state in M.Assume there exists a DFA M for which L(M) = L.Steps to prove a Language is not Regular (using DFA): Minimization Problem: Does a DFA have the minimum number of state for a given language?Īs there are algorithms to solve all these problems in linear time O(N) for DFA, this makes DFA is very useful model in Theory of Computation.Inclusion Problem: Does the language recognized by one DFA included in language recognized by another DFA.Equality Problem: Does two DFAs recognize the same language.Universality problem: Does a DFA accept all strings?.Emptiness Problem: Does a DFA accept any string?.There are other similar problems which can be solved using a DFA: If p belongs to F, then return YES else return NO.ĭFA Membership Problem can be solved in Linear Time O(N).DFA Membership ProblemĭFA Membership Problem is the problem to determine if a given word belongs to a Language L which is generated using DFA M. This summarize the properties of Deterministic Finite Automaton. DFA is closed under the following operation:.Deterministic Finite Automaton is always complete that is transition from every state has been defined for every possible input.It can be modeled using Deterministic Finite Automaton (DFA). A model of Computation is called Deterministic if there is only one choice at every step for a given input.So, if there is a Deterministic Finite Automaton M for L, there exists another Deterministic Finite Automaton N for ~L.


Δ is the transition function and is denoted for the following table: δ Examples of DFAį = is the set of accept states A language L is known as DFA Recognizable if there exists a DFA M such that L = L(M).ĭFA has resulted in the discovery of Knuth Morris Pratt Algorithm in 1976 which is a very popular string searching algorithm today.M accepts w if there is a sequence of states which starts at q 0 and ends at an accept state by processing all characters in w. Let w be a string in Σ*: w = a 1a 2.a N.L(M) is the language accepted by a given DFA M.F is a super subset of Q and is the set of accept states.q 0 belongs to Q and it is the start state.
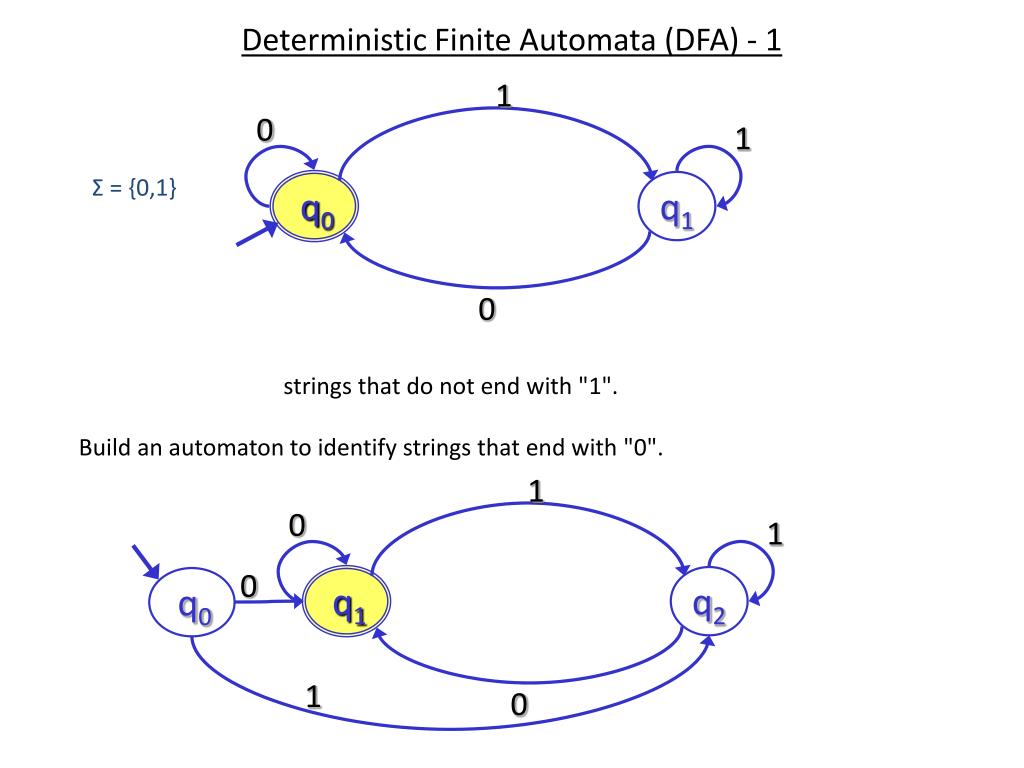
#CONSTRUCT A DETERMINISTIC FINITE AUTOMATON HOW TO#
How to prove a Language is not Regular? (using DFA).This is one of the most useful theoretical computation model. Deterministic Finite Automaton ( DFA) is the simplest version of Finite Automaton and is used to accept Regular Languages in Theory of Computation.


 0 kommentar(er)
0 kommentar(er)
